Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`

Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`

4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`

Формулы корней тригонометрических уравнений в таблице
Для синуса: Для косинуса:
Для косинуса: Для тангенса и котангенса:
Для тангенса и котангенса: Формулы решения уравнений, содержащих обратные тригонометрические функции:
Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя , преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`\frac {sin^2 x}{cos^2 x}+\frac{sin x cos x}{cos^2 x} — \frac{2 cos^2 x}{cos^2 x}=0`
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:
`\frac a{sqrt {a^2+b^2}} sin x +` `\frac b{sqrt {a^2+b^2}} cos x =` `\frac c{sqrt {a^2+b^2}}`.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a{sqrt {a^2+b^2}}=cos \varphi`, ` \frac b{sqrt {a^2+b^2}} =sin \varphi`, `\frac c{sqrt {a^2+b^2}}=C`, тогда:
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:
`\frac {3 sin x} {sqrt {3^2+4^2}}+` `\frac{4 cos x}{sqrt {3^2+4^2}}=` `\frac 2{sqrt {3^2+4^2}}`
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`sin (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac {sin x}{1+cos x}=1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
`\frac {sin x}{1+cos x}=` `\frac {(1-cos x)(1+cos x)}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {1-cos^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {sin^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}-` `\frac {sin^2 x}{1+cos x}=0`
`\frac {sin x-sin^2 x}{1+cos x}=0`
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Примеры:
\(2\sin{x} = \sqrt{3}\)
tg\({3x}=-\) \(\frac{1}{\sqrt{3}}\)
\(4\cos^2x+4\sinx-1=0\)
\(\cos4x+3\cos2x=1\)
Как решать тригонометрические уравнения:
Любое тригонометрическое уравнение нужно стремиться свести к одному из видов:
\(\sint=a\), \(\cost=a\), tg\(t=a\), ctg\(t=a\)
где \(t\) – выражение с иксом, \(a\) – число. Такие тригонометрические уравнения называются простейшими . Их легко решать с помощью () или специальных формул:
Инфографику о решении простейших тригонометрических уравнений смотри здесь: , и .
Пример . Решите тригонометрическое уравнение \(\sinx=-\)\(\frac{1}{2}\).Решение:
Ответ: \(\left[ \begin{gathered}x=-\frac{π}{6}+2πk, \\ x=-\frac{5π}{6}+2πn, \end{gathered}\right.\)\(k,n∈Z\)
Что означает каждый символ в формуле корней тригонометрических уравнений смотри в .
Внимание! Уравнения \(\sinx=a\) и \(\cosx=a\) не имеют решений, если \(a ϵ (-∞;-1)∪(1;∞)\). Потому что синус и косинус при любых икс больше или равны \(-1\) и меньше или равны \(1\):
\(-1≤\sin x≤1\) \(-1≤\cosx≤1\)
Пример
. Решить уравнение \(\cosx=-1,1\).
Решение:
\(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Ответ
: решений нет.
Пример . Решите тригонометрическое уравнение tg\(x=1\).
Решение:
|
|
Решим уравнение с помощью числовой окружности. Для этого: |
Пример
. Решите тригонометрическое уравнение \(\cos(3x+\frac{π}{4})=0\).
Решение:
|
|
Опять воспользуемся числовой окружностью. \(3x+\)\(\frac{π}{4}\) \(=±\)\(\frac{π}{2}\) \(+2πk\), \(k∈Z\) \(3x+\)\(\frac{π}{4}\) \(=\)\(\frac{π}{2}\) \(+2πk\) \(3x+\)\(\frac{π}{4}\) \(=-\)\(\frac{π}{2}\) \(+2πk\) 8) Как обычно в уравнениях будем выражать \(x\). \(3x=-\)\(\frac{π}{4}\)
\(+\)\(\frac{π}{2}\)
\(+2πk\) \(3x=-\)\(\frac{π}{4}\)
\(+\)\(\frac{π}{2}\)
\(+2πk\) |
Сводить тригонометрические уравнения к простейшим – задача творческая, тут нужно использовать и , и особые методы решений уравнений:
- Метод (самый популярный в ЕГЭ).
- Метод .
- Метод вспомогательных аргументов.
Рассмотрим пример решения квадратно-тригонометрического уравнения
Пример . Решите тригонометрическое уравнение \(2\cos^2x-5\cosx+2=0\)Решение:
|
\(2\cos^2x-5\cosx+2=0\) |
Сделаем замену \(t=\cosx\). |
|
Наше уравнение превратилось в типичное . Можно его решить с помощью . |
|
|
\(D=25-4 \cdot 2 \cdot 2=25-16=9\) |
|
|
\(t_1=\)\(\frac{5-3}{4}\) \(=\)\(\frac{1}{2}\) ; \(t_2=\)\(\frac{5+3}{4}\) \(=2\) |
Делаем обратную замену. |
|
\(\cosx=\)\(\frac{1}{2}\); \(\cosx=2\) |
Первое уравнение решаем с помощью числовой окружности. |
 |
Запишем все числа, лежащие на в этих точках. |
Пример решения тригонометрического уравнения с исследованием ОДЗ:
Пример(ЕГЭ) . Решите тригонометрическое уравнение \(=0\)|
\(\frac{2\cos^2x-\sin{2x}}{ctg x}\) \(=0\) |
Есть дробь и есть котангенс – значит надо записать . Напомню, что котангенс это фактически дробь: ctg\(x=\)\(\frac{\cosx}{\sinx}\) Потому ОДЗ для ctg\(x\): \(\sinx≠0\). |
|
ОДЗ: ctg\(x ≠0\); \(\sinx≠0\)
\(x≠±\)\(\frac{π}{2}\) \(+2πk\); \(x≠πn\); \(k,n∈Z\) |
Отметим «нерешения» на числовой окружности. |
|
\(\frac{2\cos^2x-\sin{2x}}{ctg x}\) \(=0\) |
Избавимся в уравнении от знаменателя, умножив его на ctg\(x\). Мы можем это сделать, так как выше написали, что ctg\(x ≠0\). |
|
\(2\cos^2x-\sin{2x}=0\) |
Применим формулу двойного угла для синуса: \(\sin{2x}=2\sinx\cosx\). |
|
\(2\cos^2x-2\sinx\cosx=0\) |
Если у вас руки потянулись поделить на косинус – одерните их! Делить на выражение с переменной можно если оно точно не равно нулю (например, такие: \(x^2+1,5^x\)). Вместо этого вынесем \(\cosx\) за скобки. |
|
\(\cosx (2\cosx-2\sinx)=0\) |
«Расщепим» уравнение на два. |
|
\(\cosx=0\); \(2\cosx-2\sinx=0\) |
Первое уравнение с решим с помощью числовой окружности. Второе уравнение поделим на \(2\) и перенесем \(\sinx\) в правую часть. |
 |
|
|
\(x=±\)\(\frac{π}{2}\) \(+2πk\), \(k∈Z\). \(\cosx=\sinx\) |
Корни, которые получились не входят в ОДЗ. Поэтому их в ответ записывать не будем. |
|
Опять используем окружность. |
|
|
|
Эти корни не исключаются ОДЗ, поэтому можно их записывать в ответ. |
Простейшими тригонометрическими уравнениями называют уравнения
Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a
Уравнение cos (x) = a

Объяснение и обоснование
- Корни уравнения cosx = а. При | a | > 1 уравнение не имеет корней, по-скольку | cosx | < 1 для любого x (прямая y = а при а > 1 или при а < -1 не пересекает график функцииy = cosx).
Пусть | а | < 1. Тогда прямая у = а пересекает график функции
у = cos х. На промежутке функция y = cos x убы-вает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = а имеет на этом промежутке только один корень, который по опреде-лению арккосинуса равен: x 1 = arccos а (и для этого корня cos x = а).
Косинус — четная функция, поэтому на промежутке [-п; 0] уравнение cos x = а также имеет только один корень — число, противоположное x 1 , то есть
x 2 = -arccos а.
Таким образом, на промежутке [-п; п] (длиной 2п) уравнение cos x = а при | а | < 1 имеет только корни x = ±arccos а.
Функция y = cos x периодическая с периодом 2п, поэтому все остальные корни отличаются от найденных на 2пп (n € Z). Получаем следующую фор-мулу корней уравнения cos x = а при
x = ±arccos а + 2пп, n £ Z.
- Частные случаи решения уравнения cosx = а.
Полезно помнить специальные записи корней уравнения cos x = а при
а = 0, а = -1, а = 1, которые можно легко получить, используя как ори-ентир единичную окружность.
Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответ-ствующей точкой единичной окружности является точка A или точка B.
Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C, следовательно,
x = 2πп, k € Z.
Также cos х = —1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, х = п + 2пn,



Уравнение sin (x) = a


Объяснение и обоснование
- Корни уравнения sinx = а. При | а | > 1 уравнение не имеет корней, по-скольку | sinx | < 1 для любого x (прямая y = а на рисунке при а > 1 или при а < -1 не пересекает график функции y = sinx).
Захарова Людмила Владимировна
МБОУ «Средняя общеобразовательная школа № 59» г. Барнаула
учитель математики
[email protected]
№1 Простейшие тригонометрические уравнения
Цель: 1. Вывести формулы решений простейших тригонометрических уравнений вида sinx =a, cosx=a, tgx=a, ctgx=a;
2. Научиться решать простейшие тригонометрические уравнения с помощью формул.
Оборудование: 1) Таблицы с графиками тригонометрических функций у= sinx, у=cosx, у=tgx, у=ctgx; 2) Таблица значений обратных тригонометрических функций; 3) Сводная таблица формул для решения простейших тригонометрических уравнений.
План урока-лекции :
1 .Вывод формул корней уравнения
а ) sinx =a,
б ) cosx=a ,
в ) tgx=a ,
г) ctgx=а .
2 . Устная фронтальная работа по закреплению полученных формул.
3 . Письменная работа по закреплению изученного материала
Ход урока.В алгебре, геометрии, физике и других предметах мы сталкиваемся с разнообразными задачами, решение которых связано с решением уравнений. Мы изучили свойства тригонометрических функций, поэтому естественно обратиться к уравнениям, в которых неизвестное содержится под знаком функций
Определение: Уравнения вида sinx = a , cosx = a , tgx = a , ctgx = а называются простейшими тригонометрическими уравнениями.
Очень важно научиться решать простейшие тригонометрические уравнения, так как все способы и приемы решения любых тригонометрических уравнений заключается в сведении их к простейшим.
Начнем с того, что выведем формулы, которые «активно» работают при решении тригонометрических уравнений.
1.Уравнения вида sinx =a .
Решим уравнение sinx =a графически. Для этого в одной системе координат построим графики функций у=sinx и у=а.
1) Если а > 1 и а sin х=а не имеет решений, так как прямая и синусоида не имеют общих точек.
2) Если -1а а пересечет синусоиду бесконечно много раз. Это означает, что уравнение sinx=a имеет бесконечно много решений.
Так как период синуса равен 2 , то для решения уравнения
sinx=a
достаточно найти все решения на любом отрезке длины 2.
, то для решения уравнения
sinx=a
достаточно найти все решения на любом отрезке длины 2.
Решением уравнения на [-/2; /2] по определению арксинуса х= arcsin a , а на х=-arcsin a . Учитывая периодичность функции у=sinx получим следующие выражения
х = -arcsin a +2n, n Z.
Обе серии решений можно объединить
Х = (-1) n arcsin a +n, nZ.
В следующих трех случаях предпочитают пользоваться не общей формулой, а более простыми соотношениями:
Если а =-1, то sin x =-1, х=-/2+2n
Если а =1, то sin x =1, x =/2+2n
Если а= 0, то sin x =0. x = n,
Пример: Решить уравнение sinx =1/2.
Составим формулы решений x=arcsin 1/2+ 2n
Х= - arcsin a+2n
Вычислим значение arcsin1/2. Подставим найденное значение в формулы решений
х= 5/6+2 n
или по общей формуле
Х= (-1) n arcsin 1/2+n,
Х= (-1) n /6+n,
2. Уравнения вида cosx=a .
Решим уравнение cosx=a также графически, построив графики функций у= cosx и у=а .

1) Если а 1, то уравнение cosx=a не имеет решений, так как графики не имеют общих точек.
2) Если -1a cosx=a имеет бесконечное множество решений.
Найдем все решения cosx=a на промежутке длины 2 так как период косинуса равен 2.
На решением уравнения по определению арккосинуса будет х= arcos a. Учитывая четность функции косинус решением уравнения на [-;0] будет х=-arcos a .
Таким образом решения уравнения cosx=a х=+ arcos a + 2 n,
В трех случаях будем пользоваться не общей формулой, а более простыми сотношениями:
Если а =-1, то cosx =-1, x =-/2+2n
Если а =1, то cosx =1, x = 2n,
Если а=0, то cosx =0. x =/2+n
Пример: Решить уравнение cos x =1/2,
Составим формулы решений x=arccos 1/2+ 2n
Вычислим значение arccos1/2.
Подставим найденное значение в формулы решений
X=+ /3+ 2n, nZ.
Уравнения вида tgx=a .

Так как период тангенса равен , то для того чтобы найти все решения уравнения tgx=a , достаточно найти все решения на любом промежутке длины . По определению арктангенса решение уравнения на (-/2; /2) есть arctga . Учитывая период функции все решения уравнения можно записать в виде
х= arctg a + n, nZ.
Пример: Решите уравнение tg x = 3/3
Составим формулу для решения х= arctg 3/3 +n, nZ.
Вычислим значение арктангенса arctg 3/3= /6, тогда
Х=/6+ n, nZ.
Вывод формулы для решения уравнения с tgx = a можно предоставить учащимся.
Пример.
Решить уравнение ctg х = 1.
х = arcсtg 1 + n, nZ,
Х = /4 + n, nZ.
В результате изученного материала учащиеся могут заполнить таблицу:
«Решение тригонометрических уравнений».
уравнение
Упражнения для закрепления изученного материала.
(Устно) Какие из записанных уравнений можно решить по формулам:
а ) х= (-1) n arcsin a +n, nZ;
б ) х=+ arcos a+ 2 n?
cos x = 2/2, tg x= 1 , sin x = 1/3, ctg x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3 , cos x = 2.
Какие из перечисленных уравнений не имеют решений?
Решите уравнения:
а) sin x = 0; д) sin x = 2/2; з) sin x = 2;
б) cos x = 2/2; е) cos x = -1/2; и) cos x = 1;
г) tg x = 3; ж) ctg x = -1; к) tg x = 1/ 3.
3. Решите уравнения:
а) sin 3x = 0; д) 2cos x = 1;
б) cos x/2 =1/2; е) 3 tg 3x =1;
г) sin x/4 = 1; ж) 2cos(2x+ /5) = 3.
При решении данных уравнений полезно записать правила для решения уравнений вида sinв x =a , и с sinв x =a , | a |1.
Sinв x =a, |a|1.
в х = (-1) n arcsin a +n, nZ,
х= (-1) n 1/в arcsin a +n/в , nZ.
Подведение итогов занятия:
Сегодня на занятии мы вывели формулы для решения простейших тригонометрических уравнений.
Разобрали примеры решения простейших тригонометрических уравнений.
Заполнили таблицу, которую будем использовать для решения уравнений.
Домашнее задание.
№2 Решение тригонометрических уравнений
Цель: Изучить методы решения тригонометрических уравнений:1) приводимых к квадратным;2) приводимых к однородным тригонометрическим уравнениям.
Развивать у учащихся наблюдательность при применении различных способов решения тригонометрических уравнений.
Фронтальная работа с учащимися .
Назовите формулы корней тригонометрических уравнений cos x=a , sin x=a , tgx = a , ctg x = a .
Решите уравнения (устно):
cos x=-1, sin x=0, tgx =0, ctg x=1, cos x=1,5, sin x=0.
Найдите ошибки и подумайте о причинах ошибок.
cos x=1/2, х=+
/6+2k, k Z.
Z.
sin x= 3/2, х= /3+k, kZ.
tgx = /4, x=1+ k, kZ.
2. Изучение нового материала.
На данном занятии будут рассмотрены некоторые наиболее часто встречающиеся методы решения тригонометрических уравнений.
Тригонометрические уравнения, приводимые к квадратным.
К этому классу могут быть отнесены уравнения, в которые входят одна функция (синус или косинус) или две функции одного аргумента, но одна их них с помощью основных тригонометрических тождеств сводится ко второй.
Например, если cоsх входит в уравнение в четных степенях, то заменяем его на 1- sin 2 x, если sin 2 x, то его заменяем на 1-cos 2 x.
Пример.
Решить уравнение: 8 sin 2 x - 6sin x -5 =0.
Решение: Обозначим sin x=t, тогда 8t 2 - 6t – 5=0,
D= 196,
T 1 = -1/2, t 2 = -5/4.
Выполним обратную замену и решим следующие уравнения.
Х=(-1) к+1 /6+ k, kZ.
Так как -5/4>1, то уравнение не имеет корней.
Ответ: х=(-1) к+1 /6+ k, kZ.
Решение упражнений на закрепление.
Решить уравнение:
1) 2sin 2 x+ 3cos x = 0;
2) 5sin 2 x+ 6cos x -6 = 0;
3) 2sin 2 x+ 3cos 2 x = -2sin x;
4) 3 tg 2 x +2 tgx-1=0.
Однородные тригонометрические уравнения.
Определение: 1) Уравнение вида a sinx + b cosx =0, (а=0, в=0) называется однородным уравнением первой степени относительно sin x и cos x.
Решается данное уравнение с помощью деления обеих его частей на
cosx 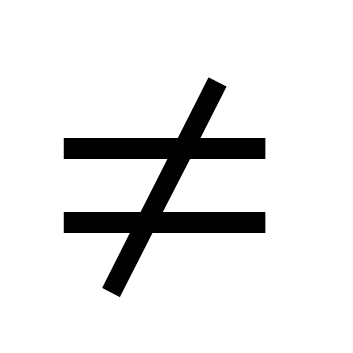 0. В результате получается уравнение
atgx+
b=0.
0. В результате получается уравнение
atgx+
b=0.
2) Уравнение вида a sin 2 x + b sinx cosx + c cos 2 x =0 называется однородным уравнением второй степени, где a, b, c какие-либо числа.
Если а=0, то уравнение решаем делением обеих частей на cos 2 x 0. В результате получаем уравнение atg 2 x+ btgx+с =0.
Замечание: Уравнение вида a sin mx + b cos mx =0 или
a sin 2 mx + b sin mx cos mx + c cos 2 mx =0 также являются однородными. Для их решения обе части уравнения делят на cos mx =0 или cos 2 mx =0
3) К однородным уравнениям могут быть сведены различные уравнения, которые первоначально не являются такими. Например, sin 2 mx + b sin mx cos mx + c cos 2 mx = d , и a sinx + b cosx = d . Для решения этих уравнений необходимо умножить правую часть на « тригонометрическую единицу» т.е. на sin 2 x + cos 2 x и выполнить математические преобразования.
Упражнения на закрепление изученного материала:
1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;
2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;
3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;
4) sin 2 x -3 sinx cosx +2 cos 2 x =0
3.Подведение итогов урока. Домашнее задание.
На данном занятии в зависимости от подготовленности группы можно рассмотреть решение уравнений вида a sin mx +b cos mx=с, где а, b,с не равны нулю одновременно.
Упражнения на закрепление:
1. 3sin x + cos x=2;
2. 3sin 2x + cos 2x= 2;
3. sin x/3 + cos x/3=1;
4. 12 sin x +5 cos x+13=0.
№ 3 Решение тригонометрических уравнений
Цель: 1) Изучить метод решения тригонометрических уравнений разложением на множители; научиться решать тригонометрические уравнения с использованием различных тригонометрических формул;
2) Проконтролировать: знание учащимися формул для решения простейших тригонометрических уравнений; умение решать простейшие тригонометрические уравнения.
План занятия:
Проверка домашнего задания.
Математический диктант.
Изучение нового материала.
Самостоятельная работа.
Подведение итогов занятия. Домашнее задание.
Ход занятия:
Проверка домашнего задания (решение тригонометрических уравнений кратко записаны на доске).
Математический диктант.
В-1
1. Какие уравнения называются простейшими тригонометрическими уравнениями?
2. Как называется уравнение вида a sinx +b cosx=0? Укажите способ его решения.
3.Запишите формулу корней уравнения tgx = a (ctg x=a ).
4. Запишите формулы корней уравнений вида cosx=a , где а =1, а =0, а =-1.
5. Запишите общую формулу корней уравнения sin x=a , | a |
6. Как решаются уравнения вида a cosx=b , | b |
В-2
1. Запишите формулы корней уравнений cosx=a ,| a |
2. Запишите общую формулу корней уравнения
= a , | a |
3. Как называются уравнения вида sin x=a , tgx = a , sin x=a ?
4.Запишите формулы корней уравнения sin x=a , если а =1, а =0, а =-1.
5.Как решаются уравнения вида sin a x=b , | b |
6. Какие уравнения называются однородными уравнениями второй степени? Как они решаются?
Изучение нового материала.
Метод разложения на множители.
Одним из наиболее употребительных методов решения тригонометрических уравнений является метод разложения на множители.
Если уравнение f(x) =0 можно представить в виде f 1 (x) f 2 (x) =0 , то задача сводится к решению двух уравнений f 1 (x)=0, f 2 (x) =0.
(С учащимися полезно вспомнить правило «Произведение множителей равно нулю, если хотя бы один из множителей равен нулю, а другие при этом имеют смысл »)
Закрепление изученного материала через решение уравнений различной сложности.
(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(самост.)
3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;
5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2-мя способами)
7) cosx+ cos3x=0; 8) sin 3x= sin 17x;
9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x
11) sin x cos5x =sin 9x cos3x sin 2x sin 2x
12) 3 cosx sin x+ cos 2 x=0(самост.)
13) 2 cos 2 x - sin (x- /2)+ tgx tg (x+/2)=0.
Самостоятельная работа.
Вариант-1 Вариант-2
1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;
2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;
3) 5 sin 2 x+ sin x cosx -2 cos 2 х=2; 3) 4sin 2 x- sin x cosx +7cos 2 х=5;
4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;
5) sin x+cosx=1. 5) sin x+cosx=2.
8. Подведение итогов урока. Домашнее задание.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х - угол, который нужно найти,
а - любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло...) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда. При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = - arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания "С" будут по плечу. С неравенствами, с отбором корней из заданного интервала... Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли...)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π /6. Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) - одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4...) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу. Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это... того... из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, - 1; 0; √3; 1/2; √3/2 и т.п. - ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да...) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово - два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там - два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн. А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Если Вам нравится этот сайт...
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)
можно познакомиться с функциями и производными.









